BP神经网络
BP神经网络(Backpropagation Neural Network)和卷积神经网络(Convolutional Neural Network,简称CNN)是两种常见的神经网络模型,它们在结构和应用方面有显著的区别。
BP神经网络是一种经典的前馈神经网络,主要由输入层、隐藏层和输出层组成。在这种网络中,每个神经元与上一层的所有神经元相连,信息只能从输入层流向输出层,不存在反馈连接。BP神经网络通过反向传播算法进行训练,通过最小化损失函数来调整网络的权值和偏置,从而实现对输入数据的分类或回归。
卷积神经网络是一种专门用于图像和视频处理的神经网络,它由卷积层、池化层和全连接层组成。卷积层通过卷积操作提取图像的特征信息,池化层用于降低特征图的维度,全连接层将特征图转化为最终的分类结果。CNN在图像分类、目标检测、语音识别等领域取得了很好的效果
我们先对BP神经网络进行介绍,先对神经网络有一个初步的认识,再进行卷积神经网络的介绍
两者的主要区别在于:
- 网络结构不同:BP神经网络主要由输入层、隐藏层和输出层组成,而卷积神经网络则是由卷积层、池化层和全连接层组成。
- 数据处理方式不同:BP神经网络通常用于处理向量型数据,如文本、声音等,而卷积神经网络则主要用于处理二维或三维数据,如图像、视频等。
- 特征提取方式不同:BP神经网络通过网络权重的调整来提取特征信息,而卷积神经网络则通过卷积操作来提取特征信息,因此卷积神经网络在图像处理任务中表现更优秀
BP神经网络理论基础
BP (Back Propagation) 神经网络是1986年由 Rumelhart 和 McClelland 为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络。
感知器网络
感知器(Perceptron)网络是早期仿生学研究的成果,在1950s由 Frank Rosenblatt 第一次引入,是一种神经网络模型。
人眼睛的视网膜由排成矩阵的光传感元件组成,这些传感元件的输出连接到一些神经元。当输入达到一定水平或者有一定类型的输入产生时,神经元就给出输出。
感知器的基本思想就在于此,即当输入的活动超过一定的内部阈值时,神经元被激活,当输入具有一定的特点时,出发速率也增加。
这里比较绕,简单来说,就是当输入达到一定的阈值的时候,神经元就会给出输出
这个在生物学上面已经有证明了,我们的激活函数很多就是模仿神经元的工作原理,所以称 "神经网络"
那么接下来就是一个比较重要的问题了,我们如何建立模型去计算呢?
我们需要模仿生物上的神经网络,建立一个个神经元然后进行连接
单个节点构成:
由输入项、权重、偏置、激活函数、输出组成
- 输入节点:x 1 , x 2 , x 3 , . . . ,
- 权重:w 1 , w 2 , w 3 , . . . ,
- 偏置:b
- 激活函数:f
- 输出节点:output

这个就是一个网络的基本结构,接下来就逐步进行解析
BP神经网络的结构与传播规则
BP神经网络是一种典型的非线性算法
BP神经网络由 输入层、隐含层(也称中间层)和 输出层 构成 ,其中隐含层有一层或者多层。每一层可以有若干个节点。层与层之间节点的连接状态通过 权重 来体现。
只有一个隐含层:传统的浅层神经网络;有多个隐含层:深度学习的神经网络。

说到这里,如果你没有接触过神经网络,可能会有点懵,这里进行一下简单的解释
输入层:不必多说,获取数据的层
隐含层:你也可以理解为训练过程,我们所有的训练就是依赖隐含层
输出层:最后的结果输出,有几个节点取决于你训练的目的,比如如果这是一个二分类问题(猫还是狗?),那么输入的数据就可能是这样的 [ 1 0 ] 或者 [ 0 1 ] ,不是猫就是狗
那么接下来的问题就是,如何进行训练呢?
BP神经网络是一种典型的非线性算法,但是呢,所有的非线性问题都可以转换为线性问题,我们可以用很多的线性来表达一个非线性,这也是我们的神经网络在实现的,每一个节点和下一层的所有节点都有连接,并且中间都经过一个线性函数,如下图:
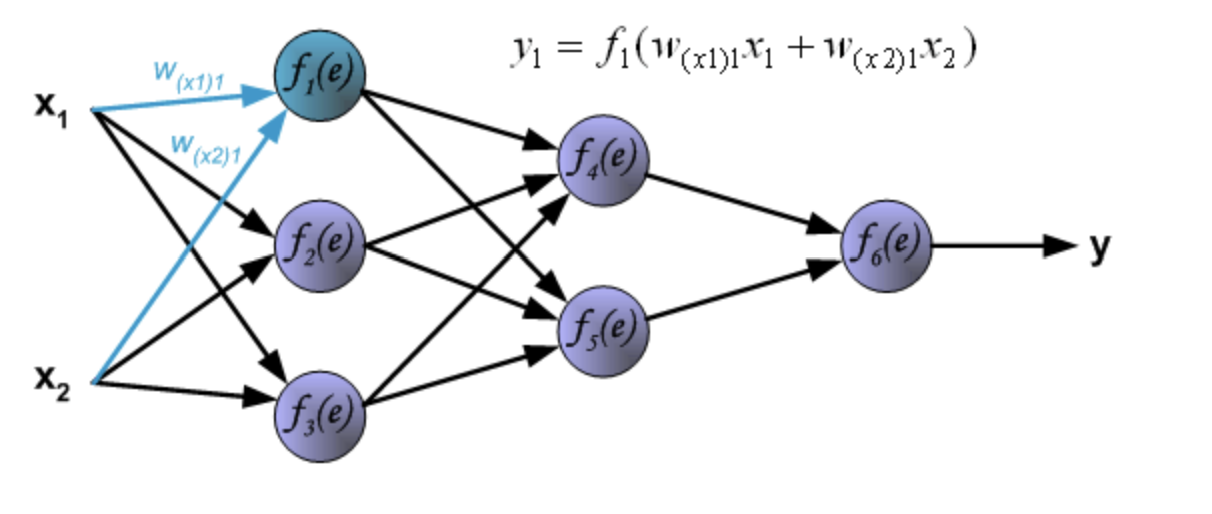
可以看到下一层的数值是多少,取决于上一层的所有数据加权和,请理解这一句话,非常重要
以此类推,每一个节点都是这样的情况,这样你就可以想象出,一个网络会有多么的复杂,计算量多么的大
在线性回归篇章中,我们论述了一个线性函数如何去拟合数据,当然,那是一个线性的数据,但是我们的数据往往不是线性的
所以这个时候我们需要非线性的函数来拟合,如下图:

所以,神经网络的本质从数学上来看,就是函数拟合,可以想象一下,如果我们将一幅图像的特征在图上用数据点来表示
那么我们的工作就是找到一个无比复杂的函数,可以很好的拟合所有特征的数据,当然,这个数据量大到我们无法描述
因为图像就是非常复杂的一个东西,特征、细节都无比庞大
那么你已经简单的了解的神经网络的组成和部分本质,接下来需要解决的就是
神经网络是如何自己训练的?怎么像线性回归算法那样自己慢慢的收敛的?
BP神经网络的核心步骤如下,其中,实线代表正向传播,虚线代表反向传播
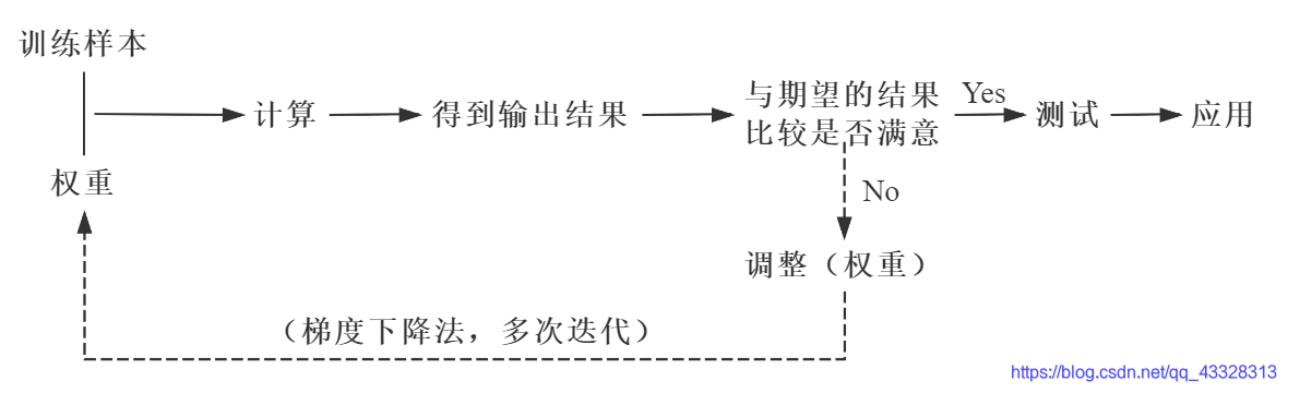
是的,我们在神经网络中就是依靠正向传播和反向传播来实现权重的更新,从而实现 "训练" 的过程
神经网络的正向传播其实我们已经讲解了,"可以看到下一层的数值是多少,取决于上一层的所有数据加权和" 在这个部分,如何计算下一层的数据以及权重和,这个部分就是正向传播的过程,所以我们的重点就是反向传播,这个也是神经网络得以实现的核心
关于正向传播和反向传播,我会在后面给出一个实战的例子来帮助理解,相信有代码的辅助会更好理解
首先先进行简单是说明,反向传播,字面意思,从结果来推过程
反向传播的过程是从结果开始的,我们通过最终得到预测值 (输出层的结果) 与 标签 (正确答案) 进行对比,将输出与期望的误差的平方和作为损失函数,逐层求出损失函数对各神经元权重的偏导数,作为目标函数对权重的梯度,根据这个计算出来的梯度来修改权重,网络的学习在权重修改过程中完成。误差达到期望值时,网络学习结束
偏导数的概念我们在高数里面会有学习,你可以简单的理解
在二维也就是x ,y 图像中,我们存在导数(梯度),但是只有一个方向,也就是y轴方向
这里我不想引入复杂的数学概念和计算公式,所以我们用两张图片对比来理解

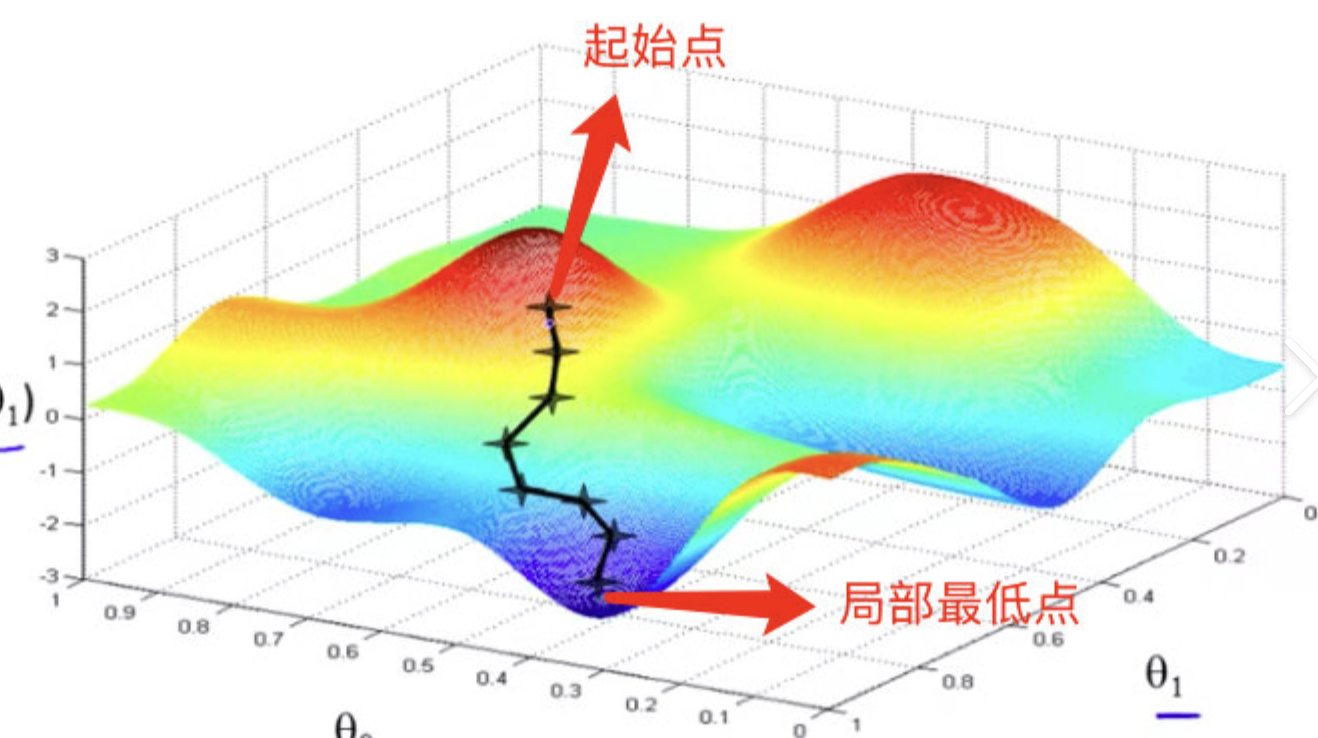
通过这两个图的对比,你可以简单将偏导数理解为 "某一个方向的梯度" 第二张图片中,我们如果要移动到局部最低点
我们需要同时对x和y进行移动,z是损失函数(Loss)的大小,我们想要最小的loss,这个时候我们想要知道x和y需要往那个方向移动
这个时候我们就对x和y求偏导,得到他们的梯度,这样就知道该往那个方向移动
简单了解了这些概念,我们正式进入反向传播的过程,求偏导这个过程不需要我们自己写,深度学习框架(如Pytorch、TensorFlow)都有自己的一套方法,直接使用就行,我们这里只是作为辅助了解
Step1 计算误差
第一步是计算神经网络的输出(预测值)和真值的误差。
图中y为我们神经网络的预测值,由于这个预测值不一定正确,所以我们需要将神经网络的预测值和对应数据的标签来比较,计算出误差。误差的计算有很多方法,比如上面提到的输出与期望的误差的平方和,熵(Entropy)以及交叉熵等。计算出的误差记为 δ δδ.
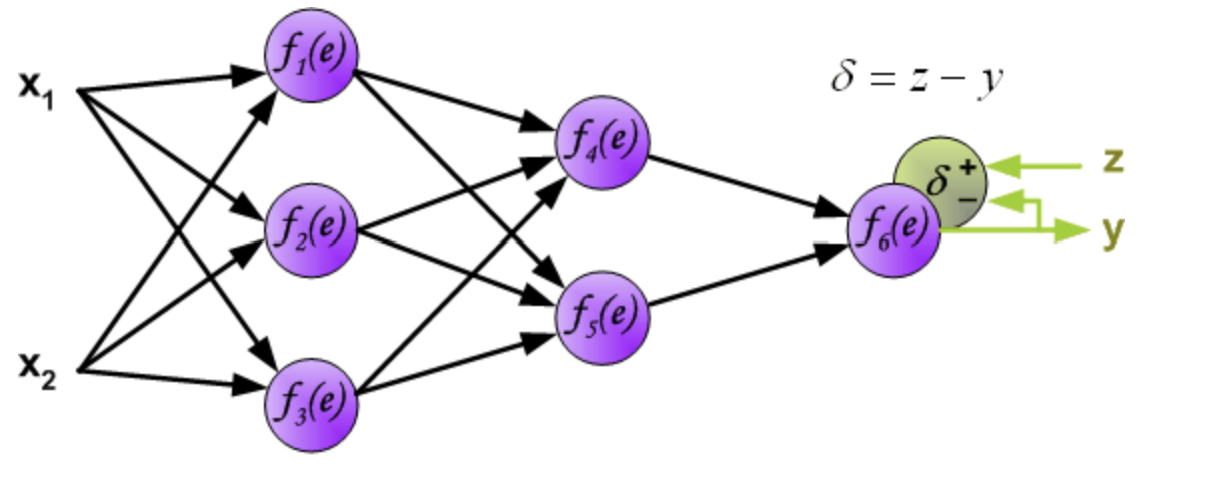
反向传播,顾名思义,是从后向前传播的一种方法。因此计算完误差后,需要将这个误差向不断的向前一层传播。向前一层传播时,需要考虑到前一个神经元的权重系数(因为不同神经元的重要性不同,因此回传时需要考虑权重系数)。
例:将误差 δ 向 f_4(e) 传播时,w_46 为 f_4(e) 的权重系数, f_4(e)的误差 δ4 = w_46 δ
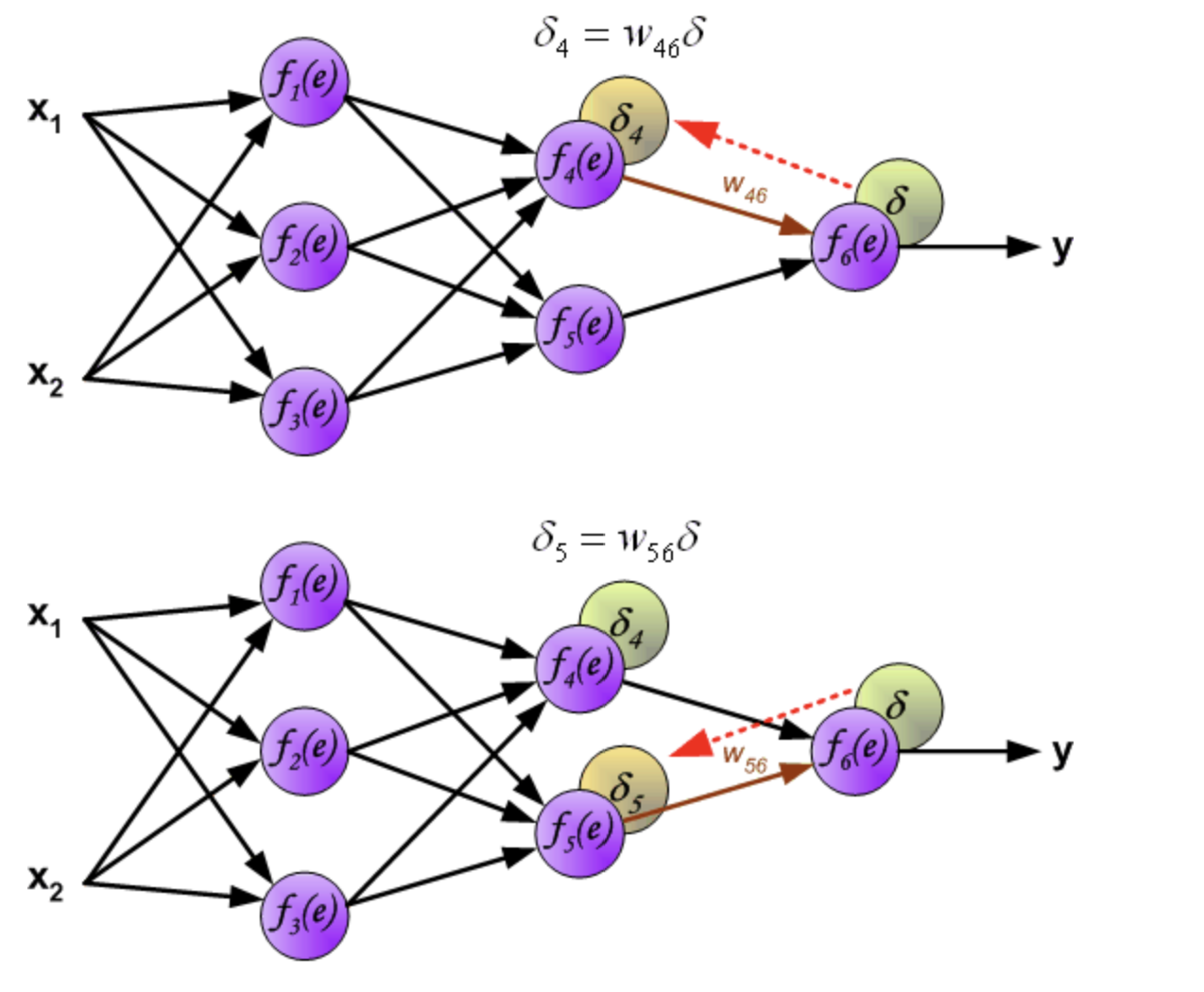
与前向传播时相同,反向传播时后一层的节点会与前一层的多个节点相连,因此需要对所有节点的误差求和。例如图中的神经元 f_1(e) 同时与 f_4(e) 和 f_5(e) 相连因此计算 f_1(e) 的误差时需要考虑后一层 f_4(e) 和 f_5(e) 的权重系数,因此δ1 = w_14 δ4 + w_15 δ5

Step2 更新权重
图中的 η 代表学习率,w ′ 是更新后的权重,通过这个式子来更新权重
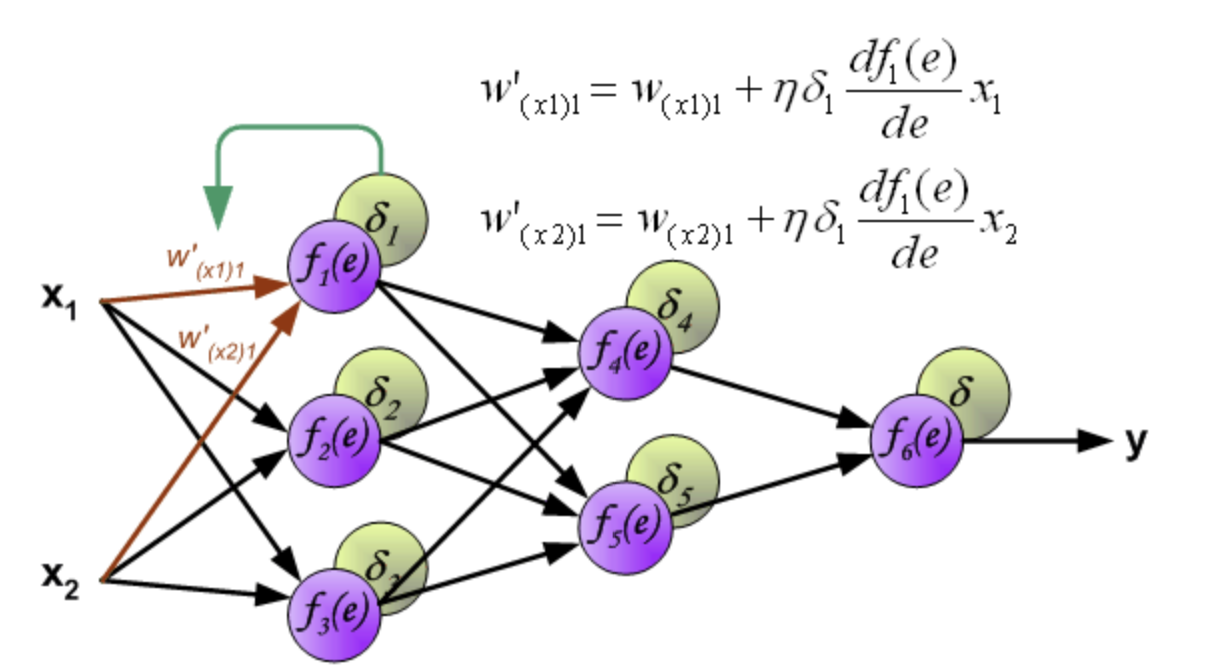
好,让我们仔细解析一下上面的过程,并回忆一下各个参数代表什么,首先,X1和X2是输入层,两个数据已经输入进来
接下来进入第一层隐含层,从第一个节点开始推,其他节点类似,原先的权重 W(x1) 加上此次训练应该变化的值就是新的权重
那么应该变化值如何计算呢?这里就是重点,η 是学习率,不解释用处,这里的δ,根据前面的推导是 δ1 = w_14 δ4 + w_15 δ5
也就是前面所有节点的误差之和,这样这个节点的权重就全部更新完成了
你说你不知道这个式子怎么来的?那你一定是忘记了数学求导法则

在这里,假设 y = f(e) = f(wx),令 e = g(w) = w*x,对应的复合函数就是:y = f(g(w))
那么y对w的导数就是
$$ dy/dw = dy/de * de/dw
$$ 那么转换一下便是
$$ df(e)/de g(w)/dw => df(e)/de x
$$ 这样我们就可以得到w的梯度信息,毕竟我们是在对w求导
当然,人家是有名字的,复合函数的导数(偏导数)的法则(链式法则)
神经网络的理论部分就是上面所述
接下来我们进入代码部分