代码演示
如果你认真看完了理论推导部分,相信你已经对神经网络有了不错的认识了,现在我们就来实现代码,当然,代码的逻辑是不可能和我们理论上推导的顺序一模一样的,都会有一套相应的代码逻辑来实现理论公式
先给出代码,如下:
import numpy as np
import math
import random
#返回[a,b]之间的随机数,用于权值初始化
def rand(a,b):
return (b-a)*random.random()+a
#返回一个m*n大小的全零矩阵
def make_matrix(m,n,fill=0.0):
mat = []
for i in range(m):
mat.append([fill] * n)
return mat
#定义sigmoid函数
def sigmoid(x):
return 1.0/(1.0+math.exp(-x))
#定义sigmoid函数的导数
def sigmoid_derivate(x):
return x*(1-x)
# BP神经网络的实现
class BPNeuralNetwork:
# 构造函数,根据网络结构设定类成员变量
def __init__(self):
self.input_n = 0
self.hidden_n = 0
self.output_n = 0
self.input_cells = []
self.hidden_cells = []
self.output_cells = []
self.input_weights = []
self.output_weights = []
# 对类成员变量进行初始化
def setup(self, ni, nh, no):
self.input_n = ni + 1
self.hidden_n = nh
self.output_n = no
self.input_cells = [1.0] * self.input_n
self.hidden_cells = [1.0] * self.hidden_n
self.output_cells = [1.0] * self.output_n
self.input_weights = make_matrix(self.input_n, self.hidden_n)
self.output_weights = make_matrix(self.hidden_n, self.output_n)
for i in range(self.input_n):
for h in range(self.hidden_n):
self.input_weights[i][h] = rand(-0.2, 0.2)
for h in range(self.hidden_n):
for o in range(self.output_n):
self.output_weights[h][o] = rand(-2.0, 2.0)
def predict(self, inputs):
for i in range(self.input_n - 1):
self.input_cells[i] = inputs[i]
for j in range(self.hidden_n):
total = 0.0
for i in range(self.input_n):
total += self.input_cells[i] * self.input_weights[i][j]
self.hidden_cells[j] = sigmoid(total)
for k in range(self.output_n):
total = 0.0
for j in range(self.hidden_n):
total += self.hidden_cells[j] * self.output_weights[j][k]
self.output_cells[k] = sigmoid(total)
return self.output_cells[:]
def back_propagate(self, case, label, learn):
# 前向预测
self.predict(case)
# 计算输出层的误差
output_deltas = [0.0] * self.output_n
for k in range(self.output_n):
error = self.output_cells[k] - label[k]
output_deltas[k] = sigmoid_derivate(self.output_cells[k]) * error
# 计算隐藏层的误差
hidden_deltas = [0.0] * self.hidden_n
for j in range(self.hidden_n):
error = 0.0
for k in range(self.output_n):
error += output_deltas[k] * self.output_weights[j][k]
hidden_deltas[j] = sigmoid_derivate(self.hidden_cells[j]) * error
# 更新隐藏层的权重
for i in range(self.input_n):
for j in range(self.hidden_n):
self.input_weights[i][j] -= learn * hidden_deltas[j] * self.input_cells[i]
# 更新输出层的权重
for j in range(self.hidden_n):
for k in range(self.output_n):
self.output_weights[j][k] -= learn * output_deltas[k] * self.hidden_cells[j]
error = 0
for o in range(len(label)):
error += 0.5 * (self.output_cells[0] - label[0]) ** 2
return error
def train(self, cases, labels, limit=100, learn=0.05):
for i in range(limit):
error = 0
for i in range(len(cases)):
label = labels[i]
case = cases[i]
error += self.back_propagate(case, label, learn)
pass
def test(self):
cases = [[0, 0], [0, 1], [1, 0], [1, 1]]
labels = [[0], [1], [1], [0]]
self.setup(2, 5, 1)
tests = [[1, 1], [0, 1], [1, 0], [1, 1]]
self.train(cases, labels, 10000, 0.5)
for test in tests:
print(self.predict(test))
if __name__ == '__main__':
nn = BPNeuralNetwork()
nn.test()
接下来再慢慢进行解释,运行结果如下:
[0.028114287942048316]
[0.9806991359805458]
[0.9805460224114356]
[0.028114287942048316]
实现目标
异或门的实现,在这里,我们这个BP神经网络实现的目标是异或门
| 输入数据 | 输出数据 |
|---|---|
| [1 1] | 0 |
| [1 0] | 1 |
| [0 1] | 1 |
| [0 0] | 0 |
既输入对应的数据,我需要得到对应的输出,这个并不难,我们让神经网络学习看看
setup
# 对类成员变量进行初始化
def setup(self, ni, nh, no):
self.input_n = ni + 1
self.hidden_n = nh
self.output_n = no
self.input_cells = [1.0] * self.input_n
self.hidden_cells = [1.0] * self.hidden_n
self.output_cells = [1.0] * self.output_n
self.input_weights = make_matrix(self.input_n, self.hidden_n)
self.output_weights = make_matrix(self.hidden_n, self.output_n)
for i in range(self.input_n):
for h in range(self.hidden_n):
self.input_weights[i][h] = rand(-0.2, 0.2)
for h in range(self.hidden_n):
for o in range(self.output_n):
self.output_weights[h][o] = rand(-2.0, 2.0)
这一个部分就是初始化的部分,将所有参数都进行初始化
值得注意的是,这里 input_n + 1 了,这意味着输入层不是2而是3,为什么要怎么做呢?
你可以自己试试,两个输入确实是难以拟合数据的(正确率下降了),加入第三个固定输入,会让我们的网络适应力更好
predict
正向传播过程,也是预测过程
def predict(self, inputs):
for i in range(self.input_n - 1):
self.input_cells[i] = inputs[i]
for j in range(self.hidden_n):
total = 0.0
for i in range(self.input_n):
total += self.input_cells[i] * self.input_weights[i][j]
self.hidden_cells[j] = sigmoid(total)
for k in range(self.output_n):
total = 0.0
for j in range(self.hidden_n):
total += self.hidden_cells[j] * self.output_weights[j][k]
self.output_cells[k] = sigmoid(total)
这里的逻辑我想不必多说,就是将所有的输入数据乘对应的权重最后加起来
back_propagate
反向传播
def back_propagate(self, case, label, learn):
# 前向预测
self.predict(case)
# 计算输出层的误差
output_deltas = [0.0] * self.output_n
for k in range(self.output_n):
error = self.output_cells[k] - label[k]
output_deltas[k] = sigmoid_derivate(self.output_cells[k]) * error
# 计算隐藏层的误差
hidden_deltas = [0.0] * self.hidden_n
for j in range(self.hidden_n):
error = 0.0
for k in range(self.output_n):
error += output_deltas[k] * self.output_weights[j][k]
hidden_deltas[j] = sigmoid_derivate(self.hidden_cells[j]) * error
# 更新隐藏层的权重
for i in range(self.input_n):
for j in range(self.hidden_n):
self.input_weights[i][j] -= learn * hidden_deltas[j] * self.input_cells[i]
# 更新输出层的权重
for j in range(self.hidden_n):
for k in range(self.output_n):
self.output_weights[j][k] -= learn * output_deltas[k] * self.hidden_cells[j]
error = 0
for o in range(len(label)):
error += 0.5 * (self.output_cells[0] - label[0]) ** 2
return error
我们进入重点,反向传播,仔细看代码,计算输出层的误差部分,你会看到它内部是进行了求导的
你可能就会有点不对劲了,怎么求误差的时候就求导了,我们再看一下更新输出层的权重,你会发现,就是公式里面的内容
和公式的计算是一模一样的,为什么我们这里求误差的时候就求导了呢?和后面隐藏层的误差计算有一定的关系
我们知道,权重w的大小能直接影响输出,w不合适那么会使得输出误差。要想直到某一个w值对误差影响的程度,可以用误差对该w的变化率来表达。如果w的一点点变动,就会导致误差增大很多,说明这个w对误差影响的程度就更大,也就是说,误差对该w的变化率越高。而误差对w的变化率就是误差对w的偏导。 所以,看下图,总误差的大小首先受输出层神经元O1的输出影响,继续反推,O1的输出受它自己的输入的影响,而它自己的输入会受到w5的影响。这就是连锁反应,从结果找根因。
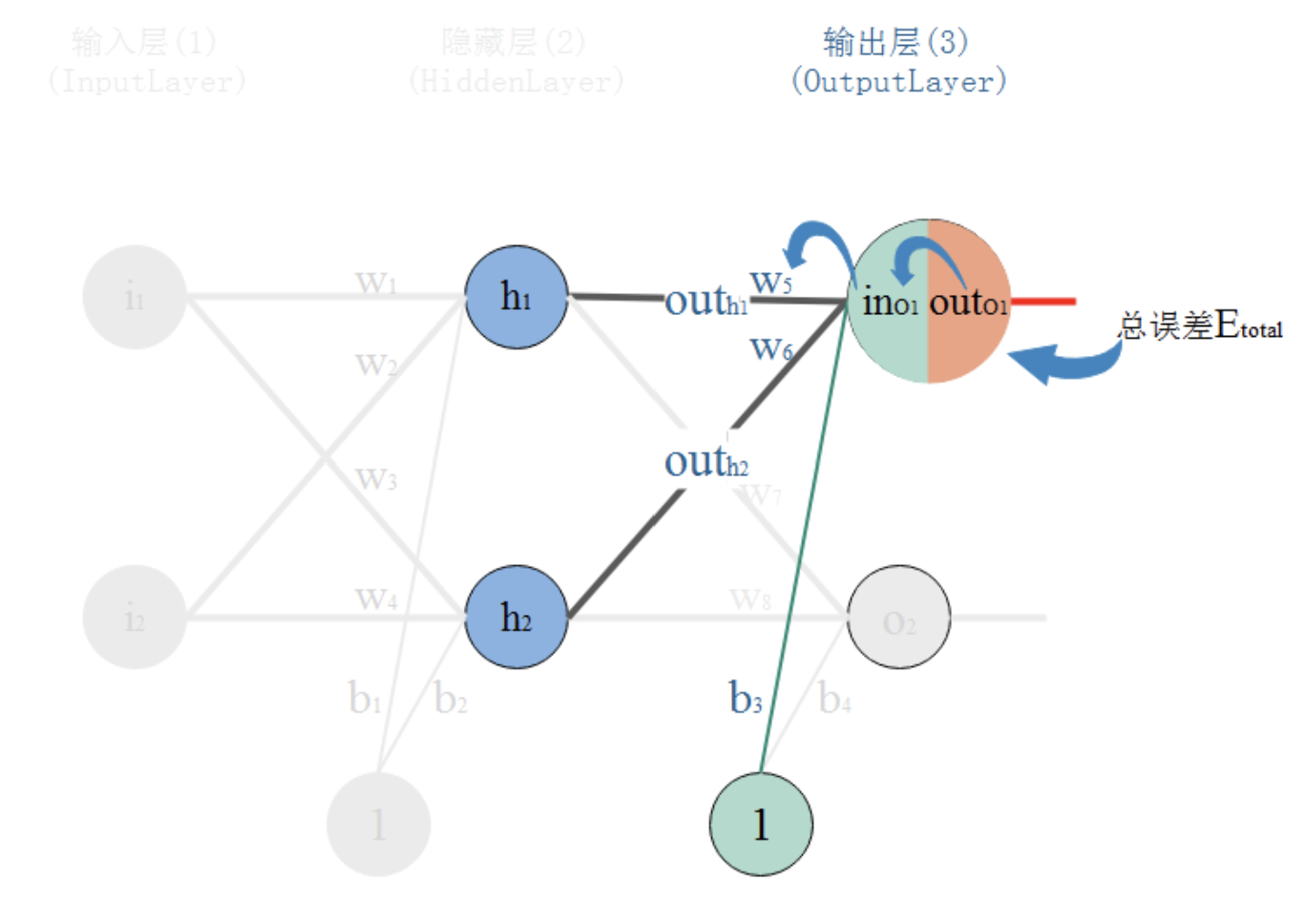

可以发现,如果我们后面要计算梯度(也就是偏导)的时候,前面也是要求导的,所以我们在这里提前先计算好梯度信息
然后保存下来,这里再到上一层的时候,直接就能拿到误差和梯度信息,这样我们就可以只关心更前面的部分,不需要再计算后面的部分
通过计算隐藏层的误差的部分,你也可以看到,如果你将最后的结果式子展开,确实有一条非常长的链式求导
这里就是不一样的地方了,我们在理论推导的时候,并不会说真正的考虑全部的计算,而是用一个函数表达前面所有的计算
但是在编写代码的时候,我们的计算逻辑是要真真切切的存在的,所有的计算都是需要写出来的,这个时候,就需要我们进行相应的改动
如果你有兴趣,对我们理论部分的式子从最后一层(输出层)开始展开
那么最后到输入层前面的时候,将会有非常长的一条求导公式
需要说的是,设计几层网络比较好的问题仍然是个黑匣子,没有理论支撑应该怎么设计网络,现在仍是经验使然
到此,整个BP神经网络就基本结束了,谢谢观看