线性回归算法

当然我介绍那么多，相信你也是比较懵逼的，所以我简单介绍一下基础概念，然后进入实战

我们将会使用 Python 来完成机器学习的任务

环境可以使用 Ananconda 来进行管理，IDE可以选择 PyCharm (完全免费) 社区版

首先，我们需要明确，我们的目的是什么

线性回归相信你并不陌生，这个是高中就会进行学习的东西，忘记了也没有关系，简单回忆一下

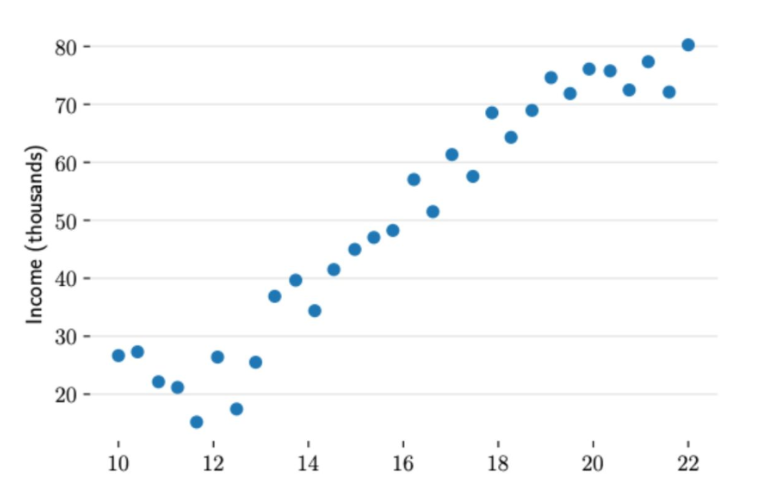
这是一幅散点图，散乱的数据，和我们实际生活中的数据一样，我们的目的便是从这些点之间进行拟合

作出一条最佳的直线，求其截距和斜率，如下图

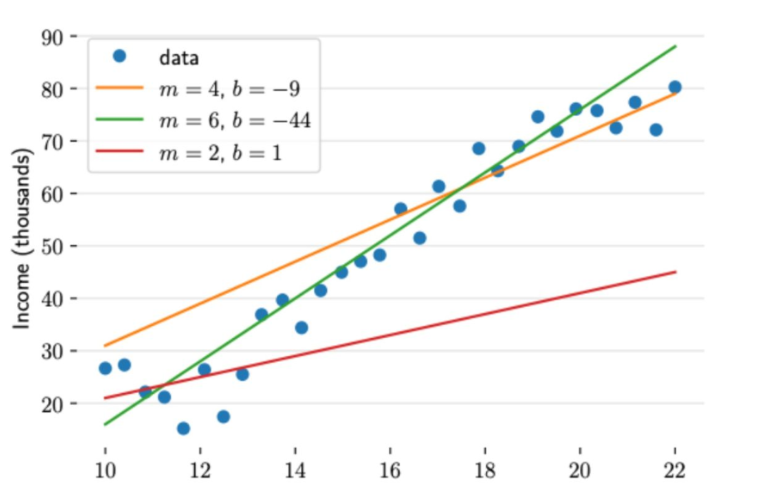
相信到这你已经回忆起来一部分了，那么让我们再进一步

这么多条直线，我们如何判断那条直线是最佳选项呢，我们需要一个方法或者说标准

是的，就是 最小二乘法 ，让我们简单回忆一下最小二乘法

最小二乘法原理

​ 在工程应用中，我们经常会用一组观测数据去估计模型的参数，模型是我们根据先验知识定下的。比如我们有一组观测数据( x i , y i ) (x_i,y_i)（一维），通过一些数据分析我们猜测y和x之间存在线性关系，那么我们的模型就可以定为：f ( x ) = k x + b

​ 这个模型只有两个参数，所以理论上，我们只需要观测两组数据建立两个方程，即可解出两个未知数。类似的，假如模型有n nn个参数，我们只需要观测n nn组数据就可求出参数，换句话说，在这种情况下，模型的参数是唯一确定解

​ 但是在实际应用中，由于我们的观测会存在误差（偶然误差、系统误差等），所以我们总会做多余观测。比如在上述例子中，尽管只有两个参数，但是我们可能会观测n nn组数据( x 1 , y 1 ) . . , ( x n , y n ) (x_1, y_1)..，这会导致我们无法找到一条直线经过所有的点，也就是说，方程无确定解

​ 于是这就是我们要解决的问题：虽然没有确定解，但是我们能不能求出近似解，使得模型能在各个观测点上达到“最佳“拟合。

​ 早在19世纪，勒让德就认为让“误差的平方和最小”估计出来的模型是最接近真实情形的。

​ 为什么就是误差平方而不是其它的，这个问题连欧拉、拉普拉斯都未能成功回答，后来是高斯建立了一套误差分析理论，从而证明了确实是使误差平方和最小的情况下系统是最优的

按照勒让德的最佳原则，于是就是求：

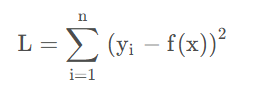
​ 这个目标函数取得最小值时的函数参数，这就是最小二乘法的思想，所谓“二乘”就是平方的意思。从这里我们可以看到，最小二乘法其实就是用来做函数拟合的一种思想。

了解了最小二乘法的原理，相信你已经有了答案，如图：

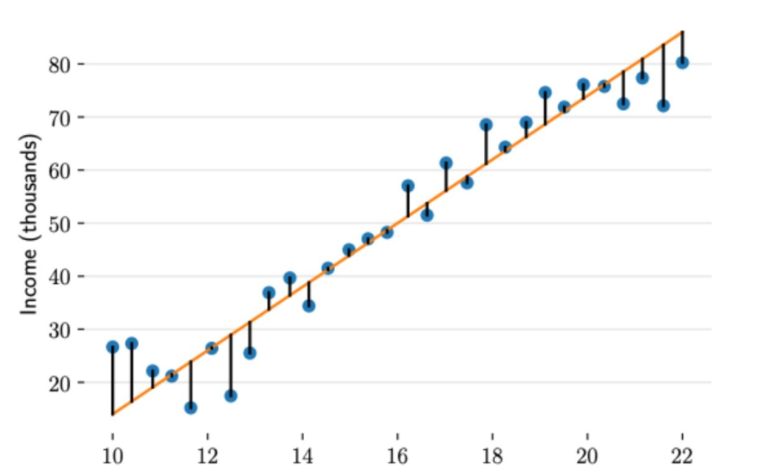
人话：

​ 所有点到直线距离的平和之和最小即可