半径求解
//=========================获取整车观测所需数据========================
// TODO: 待封装
bool Data_capture_OK = false; // 数据采集
bool Long_Short_OK = false; // 长短轴采集
/** 同时出现两个装甲板 */
if(Armor_number == 2){
double Track_Armor_diff = abs(abs(Track_Armor[0].camera_position[1])-abs(Track_Armor[1].camera_position[1]));
if (Track_Armor_diff < 0.1) {
// std::cout << "A" << std::endl;
Long_Short_OK = true;
}
// 两装甲板Y轴距离小于阈值(test)
// 进入采集模式
Data_capture_OK = true;
}
if(Data_capture_OK){
// 相机坐标系手动转换世界坐标
Eigen::Vector3d Track_1 = Track_Armor[0].camera_position;
Eigen::Vector3d Track_2 = Track_Armor[1].camera_position;
Track_1 = {Track_1[0],Track_1[2],-Track_1[1]};
Track_2 = {Track_2[0],Track_2[2],-Track_2[1]};
double angle = 180.0f/CV_PI;
这里的相机坐标系手动转换世界坐标只是为了符合我们的认知,方便后面的坐标操作
这里是判断是否可以进行采集的判断,当然这里的判断存在一定的问题,就是过于理想,如果你实际测试就会发现
同时出现两个装甲板的条件非常苛刻,甚至在陀螺的时候,基本很难捕捉到两个装甲板同时出现的情况
这里采集的数据是为了计算车的半径的、以及高低装甲板,后面发现观测不够稳定,而且我们的车高低差基本可以忽略
没有办法进行很好的测试,所以这里的数据在2024赛季上实际并没有使用,是等待优化的一个模块
对于半径的求解,我和多个队伍交流过,都认为,如果你不能保证算法的可信度以及稳定性,不如直接固定车的半径
因为目前大部分队伍的车大小都差不多,所以直接写死半径的方法在赛场上是可行的,但是不够优雅
不过基本的半径求解方法你是需要知道的,并且或许你有优化的思路和想法,可以尝试看看
我这里尝试了两种方法,下面是第一种:
/** 通过装甲板朝向角和中心世界坐标系建立Y-X下的一次函数 */
// 左装甲板一次函数
double as_angel_1 = AS.Armor_Angle(Track_Armor[0]);
double angle_1 = (90.0-Track_Armor[0].R[1]*angle)*(CV_PI/180.0f);
double K_1 = tan(angle_1);
double B_1 = Track_1[1]-K_1*Track_1[0];
// 右装甲板一次函数
double as_angel_2 = AS.Armor_Angle(Track_Armor[1]);
double angle_2 = -(90.0-abs(Track_Armor[1].R[1])*angle)*(CV_PI/180.0f);
double K_2 = tan(angle_2);
double B_2 = Track_2[1]-K_2*Track_Track_Armor2[0];
/** 使用矩阵计算联立方程求解交点 */
/** 矩阵计算
* [ 1 -K1 [ Y = [ B1
* 1 -K2 ] X ] B2 ]
*/
Eigen::Matrix<double,2,2> K;
Eigen::Matrix<double,2,1> X;
Eigen::Matrix<double,2,1> Y;
K << 1,-K_1,
1,-K_2;
Y << B_1,
B_2;
X = K.inverse()*Y;
// 计算
double R_1 = sqrt(pow(X[1]-Track_1[0],2)+pow(X[0]-Track_1[1],2));
double R_2 = sqrt(pow(X[1]-Track_2[0],2)+pow(X[0]-Track_2[1],2));
// 只有达到采集要求才会更新
if(Long_Short_OK) OB[tracking_id].update(R_1,R_2);
std::cout << "R_1: " << R_1 << " R_2:" << R_2 << std::endl;
首先需要说明的是,为什么条件如此苛刻,因为这里的半径计算是需要同时出现两块装甲板的,看下图:
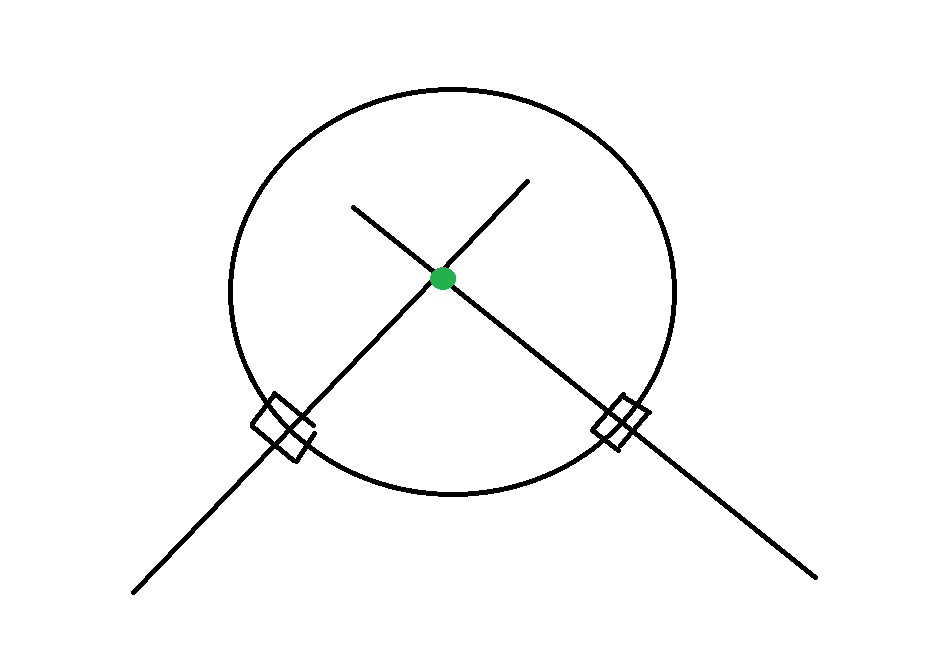
相信看到你就已经有想法了,是的,就是两个装甲板延长线交点,必然是圆形,而两个装甲板的相位差是90°
只要我们可以写出两条一次函数,联立求解,自然可以得到半径的数值,当然这是非常理想的情况,我们的观测和计算都存在误差
所以实际解算出来的数据有较大偏差,下面来看看如何进行解算
// 左装甲板一次函数
double as_angel_1 = AS.Armor_Angle(Track_Armor[0]);
double angle_1 = (90.0-Track_Armor[0].R[1]*angle)*(CV_PI/180.0f);
double K_1 = tan(angle_1);
double B_1 = Track_1[1]-K_1*Track_1[0];
首先我们看左边的装甲板,Armor_Angle这个是三分法求解Yaw的函数,使用SolvePnP解算的Yaw数据效果一样(而且这个数据是测试用的,后面忘记删了,并没有用到)
angle_1就是我们的Yaw数据,也是这里的直线和水平线的夹角,这里的坐标原点是我们的相机坐标系转成的世界坐标系
这一点需要特别注意,本质是相机坐标系,不能使用真正的世界坐标系去计算观测数据,因为世界坐标系是不动的,是难以计算的,具体为什么你可以仔细思考一下,后续的观测计算基本都是在相机坐标系下的操作,再转换为真正的世界坐标系
这里的矩阵求解联立方程的方法网上可以查到,自行学习
下面是尝试优化之后的计算
/** 三分法逼近求解半径(经过测试比延长法稳定) */
// 画出中心
double x = (Track_1[0]+Track_2[0])/2;
double y = (Track_1[1]+Track_2[1])/2;
double z = (Track_1[2]+Track_2[2])/2;
Eigen::Vector3d temp_pos = {x,-z,y}; //相机坐标系
temp_cir = AS.cam2pixel(temp_pos);
// 三分法逼近x所在位置
// R_1
double R_1_yaw = Track_Armor[0].R[1]*angle;
double R_2_yaw = Track_Armor[1].R[1]*angle;
// 补偿角度
while ((abs(R_1_yaw) + abs(R_2_yaw)) <= 90){
R_1_yaw += 0.1;
R_2_yaw -= 0.1;
}
R_1_yaw = R_1_yaw*(CV_PI/180.0f);
R_2_yaw = R_2_yaw*(CV_PI/180.0f);
double l_1 = 0.1,r_1 =0.6; // 半径范围
double eps = 1e-8; // 精度
double R_1;
while (r_1-l_1 >= eps) {
double thridPart = (r_1-l_1)/3;
double lsec = l_1 + thridPart;
double rsec = r_1 - thridPart;
// 计算当前半径距离目标的差值
double ls = Track_1[0]+sin(R_1_yaw)*lsec; // 三角函数解圆心
double rs = Track_1[0]+sin(R_1_yaw)*rsec; // 三角函数解圆心
double ls_dis = abs(abs(x)-abs(ls));
double rs_dis = abs(abs(x)-abs(rs));
if(ls_dis > rs_dis) l_1 = lsec;
else r_1 = rsec;
// std::cout << R_1_yaw*angle << std::endl;
// std::cout << ls << " " << rs << std::endl;
// std::cout << ls_dis << " " << rs_dis << std::endl;
// std::cout << l_1 << " " << r_1 << std::endl;
// std::cout << "x:" << x << " Track:" << Track_1[0] << std::endl;
}
R_1 = l_1;
// R_2
double l_2 = 0.1,r_2 =0.6; // 半径范围
double R_2;
while (r_2-l_2 >= eps) {
double thridPart = (r_2-l_2)/3;
double lsec = l_2 + thridPart;
double rsec = r_2 - thridPart;
// 计算当前半径距离目标的差值
double ls = Track_2[0]+sin(R_2_yaw)*lsec; // 三角函数解圆心
double rs = Track_2[0]+sin(R_2_yaw)*rsec; // 三角函数解圆心
double ls_dis = abs(abs(x)-abs(ls));
double rs_dis = abs(abs(x)-abs(rs));
if(ls_dis > rs_dis) l_2 = lsec;
else r_2 = rsec;
}
R_2 = l_2;
// 待测试
double Trisection_R_1 = Solve_Radius(Track_Armor[0],R_1_yaw,x);
double Trisection_R_2 = Solve_Radius(Track_Armor[1],R_2_yaw,x);
这里是将计算的方法从一次函数求解换成三分法下降求解圆心,这个方法会更加稳定一些,但是无论哪种方法都绕不开Yaw数据和坐标数据,所以这两个数据一旦不稳定,出现波动,这一部分相应也会出现很大的误差,也正是因为难以排除干扰,所以计算出来的数据并不理想,反而固定值更加稳定,Trisection_R_1、Trisection_R_2 并没有使用
如果想要优化这一部分,你需要让数据来源更加可靠,比如给Yaw的数据加一个卡尔曼滤波,或者优化求解Yaw的方法
对于坐标的话,我的建议是尽量减小三维坐标对整体的影响,因为三维坐标并不是绝对稳定的,特别是距离数据(也就是Y轴)
这个数据来源是不可靠的,在装甲板旋转的时候,可以看到距离的数据跳变是较大的,但是X轴和Z轴数据是相对可靠的,因为这两个数据是不用通过复杂的计算的,在图像上就可以大致看出来,所以这两个数据是相对稳定很多的
关于这一部分的话,我的优化建议是先将数据优化,让数据变的稳定一些,然后进行建模,简单来说就是用一个多项式拟合数据,比如弹道,就可以通过大量的测试,得到距离和抬枪角度的数据,通过多项式拟合的方法去简单建立模型,用Matlab或者Origin都可以简单做到
关于怎么测试这些数据的方法,你可以将距离数据打印出来,然后让车旋转,最后将数据复制粘贴到 Exel 表格之中,使用表格自带的画图功能,将数据画出来,就可以直观的看到数据反馈,也可以把数据输出保存到文件里面,效果相同
视觉直观反馈数据的方法事实上是比较少的,也很难建立起体系,通过图像分析问题的难度是较高的
比较优的方法也是我去深大见过的就是使用QT绘制一个图表来进行反馈